자연수는 약수의 개수에 따라 1과 소수, 그리고 합성수로 구분합니다.
*1 : 약수의 개수가 1개인 수소수 : 약수의개인
*합성수 : 약수의 개수가 3개 이상인 수
*소수 : 1과 자기 자신만으로 나누어떨어지는
1보다 큰 자연수
에라토스테네스는 소수를 찾아내는 방법을 발견했는데 이것을 에라스토의 체라고 하고, 설명하면 다음과 같습니다.
본인이 구하고자 하는 구간의 모든 자연수를 차례로 나열한 후
*1은 소수가 아니므로 지워줍니다.
*2는 소수이므로 ○표시를 하고, 2의 배수를 다 지워줍니다.
*남아있는 수 가운데 3은 소수이므로 ○표시를 하고, 3의 배수를 다 지워줍니다.
*남아있는 수 가운데 5는 소수이므로 ○표시를 하고, 5의 배수를 다 지워줍니다.
이런 과정을 계속 반복하면 구하고자 하는 구간의 수 중에서 소수만 남고 합성수들은 다 지워집니다
2 이상 100 이하의 소수 ( 25개 )
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
101 이상 200 이하의 소수 ( 20개 )
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 197, 199
201 이상 300 이하의 소수 ( 16개 )
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293
301 이상 400 이하의 소수 ( 16개 )
307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397,
401 이상 500 이하의 소수 ( 17개 )
401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499
501 이상 600 이하의 소수 ( 14개 )
503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599
601 이상 700 이하의 소수 ( 15개 )
601, 607, 613, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691
701 이상 800 이하의 소수 ( 14개 )
701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797
801 이상 900 이하의 소수 ( 15개 )
809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887
901 이상 1000 이하의 소수 ( 14개 )
907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
이렇게 1000 이하의 자연수 중에 소수는 총 168개가 있다고 합니다.
소수를 이용한 골드바하의 추측을 확인해 볼까요


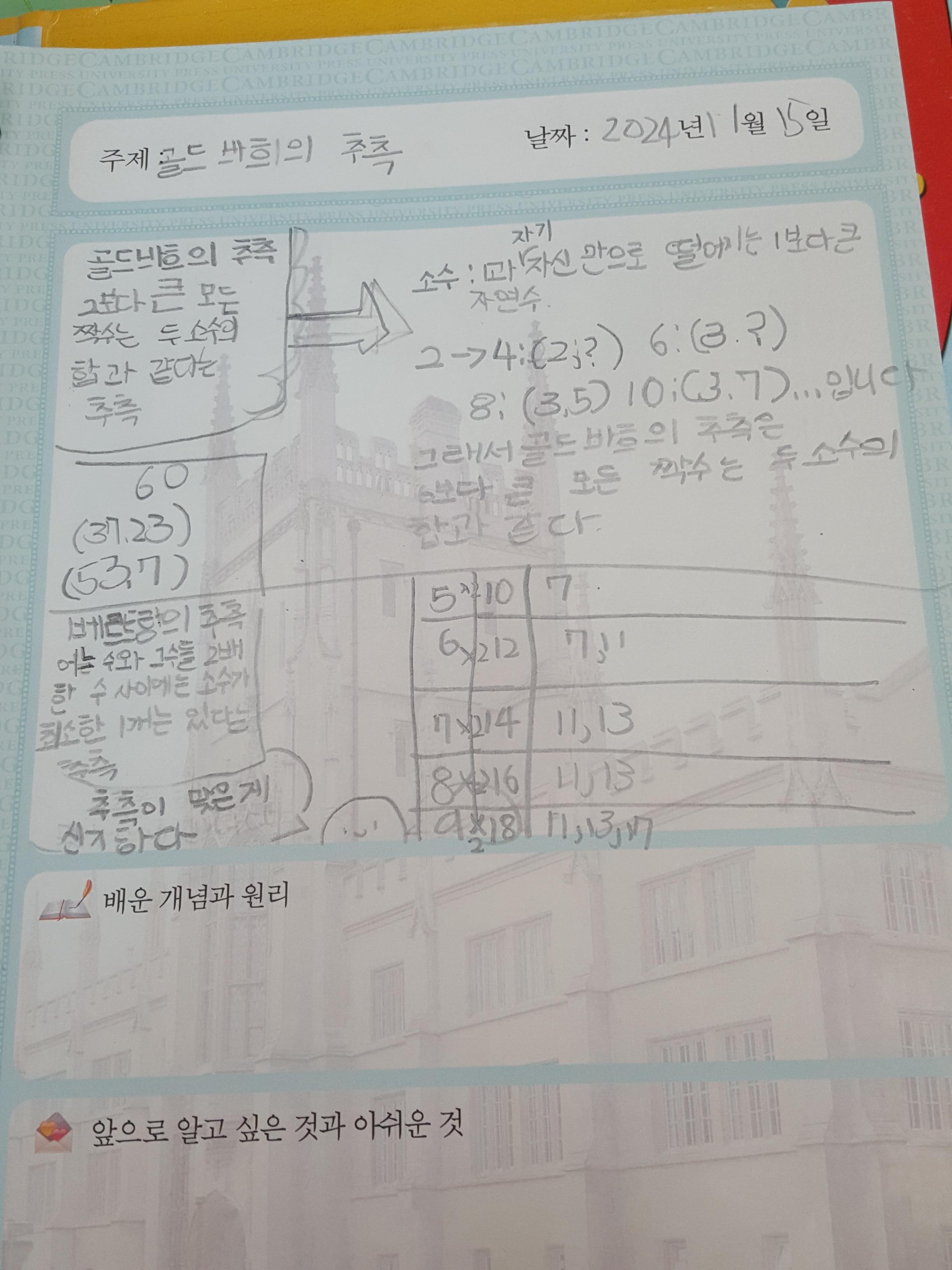
★골드바흐의 추측
2보다 큰 모든 짝수는 두 소수의 합과
같다는 추측을 했습니다.
12(5,7)
60(7,53)
100(47,53)...........
증명이 되었을까요????
★베르트랑의 추측
어느 수와 그 수를 2배 한 수 사이에는
소수가 최소한 1개 있다는 추측을 했습니다.
| 수 | 2배수 | 두 수 사이의 소수 |
| 2 | 4 | 3 |
| 3 | 6 | 5 |
| 4 | 8 | 5, 7 |
| 5 | 10 | 7 |
| 6 | 12 | 7, 11 |
| 10 | 20 | 11,13,17,19 |
1850년 옳은 것으로 판명되어
『베르트랑의 공리』라고 불린답니다



https://blog.naver.com/ssisahoy
포스코 아이리더스쿨 : 네이버 블로그
-유치원2급, 1급, 원감, 원장자격증 취득, *<강서교육청 교육장>상 *< 서울특별시 교육감>상 수상 -교육게임 지도자 자격증 -독서지도사 -스토리텔링지도사 -초등수학 지도사-융합코딩지도사자격
blog.naver.com
'캠브리지수학4학년' 카테고리의 다른 글
| 이상한 고리/뫼비우스띠/캠브리지수학/동탄 (0) | 2024.10.29 |
|---|---|
| 일곱 개의 다리/한붓그리기/캠브리지수학/동탄 (10) | 2024.10.28 |
| 캠브리지수학 - 소수(파리 올림픽에서 소수 찾기) (7) | 2024.08.01 |
| 캠브리지 수학 - 피보나치수열 (0) | 2024.07.16 |
| 로마 수의 규칙 (0) | 2024.07.06 |