◈개념교구 - 스도쿠, 솔리테어
◈게임교구 - 초콜릿 픽스, 피빗, 셈셈 눈썰매장, 루미큐브
출처 - 위키백과
스도쿠는 '숫자가 겹치지 않아야 한다' 또는
'한 자릿수'라는 뜻으로
18세기의 스위스 수학자
레온하르트 오일러(Leonhard Euler)가 고안한
'라틴 방진(Latin square)'에서 유래되었다고 합니다.
게임 규칙이 단순하지만
머리를 많이 써야 하는 지능형 퍼즐입니다.
스도쿠의 비어있는 숫자들을 찾다 보면
논리적인 판단력과 추론 능력이
자연스럽게 길러지게 됩니다.
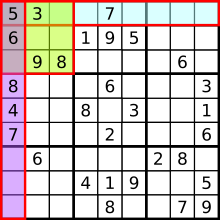
규칙
1~9까지의 숫자를
* 각각의 가로줄에 숫자가 하나도 겹치지 않게 들어가야 합니다.
* 각각의 세로줄에 숫자가 하나도 겹치지 않게 들어가야 합니다.
* 굵은 선( 3×3 칸에)으로 이루어진 9칸에 숫자가 하나도 겹치지 않게 들어가야 합니다.



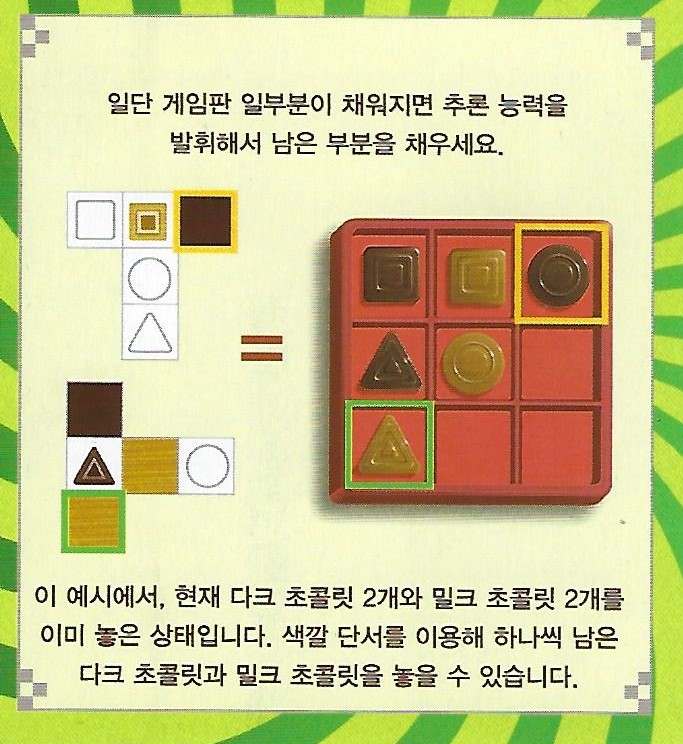
게임 교구 - 초콜릿 픽스
추론 논리 보드게임
문제에 나와 있는 단서를 이용해 게임판에
초콜릿 9개를 채우세요
주어진 정보에 따라 각각의 초콜릿을
알맞은 자리에 놓으세요
초콜릿 세트를 완성하면 문제 뒷면에 나와 있는
해답을 보고 제대로 맞췄는지 확인하세요


























스도쿠의 역사는 1892년까지 거슬러 올라갑니다.
프랑스의 일간지 《Le Siècle》가 두 자리 숫자를 이용한
스도쿠와 같은 방식의 퍼즐을 게재했습니다.
1895년에는 다른 일간지 《 La France 》가 한 자리 숫자로 9×9의 바둑판을 채우는 퍼즐을 게재했지만,
여기선 3×3블록 룰은 없었습니다.
이 퍼즐들은 이따금 프랑스 몇몇 신문에 매주 게재되었지만
얼마 안 가서 제1차 세계대전 전후로 그 모습이 사라졌습니다.
스도쿠는 18세기 스위스 수학자 레온하르트 오일러가 창안한 Latin Square를 기반으로 하여
1979년 당시 74세의 건축가였던 미국의 Howard Garns가 현재의 모습으로 변형하여
1979년 5월 미국의 '델 매거 진즈'(Dell Magazines)가 잡지 《 Dell Pencil Puzzles & Word Games 》에 "Number Place"로 소개된 것이 시초이나,
1984년 4월 일본의 출판사인 '니코리'(ニコリ, Nikoli)가 출판한 잡지 《퍼즐 통신 니코리》(パズル通信ニコリ)[2]에 '스도쿠'라는 이름을 붙여 수록하면서
대중에게 보급되기 시작하여 2005년 무렵에 이르러 온 세계로 퍼져 나갔습니다.
출처 - 위키백과





게임 교구 - PIVIT피빗
색과 무늬로 연결하는 스피드 전략 게임
시각적 사고 능력 향상 게임




















개념교구 - 솔리테어
솔리테어는 독일의 수학자
라이프니츠가 만들었습니다.
33개의 구멍이 있는데 가운데
한곳만 빼고 모두 구멍에
구슬을 채워 넣고 하나의 구슬을 선택하여
다른 구슬을 넘어가면서
이때 밑에 있었던 구슬을 뺍니다.
가로, 세로로만 넘어갈 수 있으며
대각선은 안됩니다.
최종 목표는 하나의 구슬만 남기는 것입니다.
게임의 규칙은 단순하지만
고도의 전략을 요하는 게임으로,
구슬을 공간 이동한 후의 상황을
예측하고 추론하는 능력과
공간지각력 및 문제해결 능력이 발달합니다.
♥게임 규칙
(1) 하나의 구슬을 선택하여 다른 구슬을 넘어갑니다.
(2) 넘어갈 때 밑에 있었던 구슬을 뺍니다.
(3) 한 번에 하나의 구슬만 넘어갈 수 있습니다.
(4) 가로와 세로로만 넘어갈 수 있습니다.
대각선은 안됩니다.
(5) 더 이상 넘어갈 구슬이 없으면 멈춥니다.Bit
(6) 제일 마지막에 구슬이 한 개 남으면 성공입니다











게임 교구 - 셈셈 눈썰매장
나눗셈하여 몫만큼 이동하여
도착점에 먼저 도착하면 승리합니다.





















개념교구 - 솔리테어
♥게임 규칙
(1) 하나의 구슬을 선택하여 다른 구슬을 넘어갑니다.
(2) 넘어갈 때 밑에 있었던 구슬을 뺍니다.
(3) 한 번에 하나의 구슬만 넘어갈 수 있습니다.
(4) 가로와 세로로만 넘어갈 수 있습니다.
대각선은 안됩니다.
(5) 더 이상 넘어갈 구슬이 없으면 멈춥니다.Bit
(6) 제일 마지막에 구슬이 한 개 남으면 성공입니다.
구슬 한 개만 남기기에 도전해 보고,
구슬의 이동 경로를 써보세요






















게임 교구 - 루미큐브
세트(그룹과 연속)를 만들어
자신의 타일을 가장 먼저 테이블 위에
내려놓은 사람이 승리합니다
















욕실의 타일은 왜 정사각형일까
정사각형 타일 이외에 직사각형의 타일도 볼 수 있지만
그 외의 사각형(평행사변형, 사다리꼴, 마름모, 연모 양, 일반 사각형, 둔각 사각형)의 타일은 본 적이 없을 거예요
왜 그럴까요?
그에 대한 이유로 두 가지를 생각할 수 있는데,
첫째, 정사각형, 직사각형 이외의 사각형은
평면을 빈틈없이 메울 수가 없고,
둘째, 모서리 처리와 타일의 제조 비용이 너무 많이 들어서
경제적이지 못하다는 점입니다.
하지만 첫째의 경우는
사각형의 내각의 합은 360도이기 때문에
어떠한 사각형으로도 평면을 빈틈없이 메울 수 있습니다.
둘째의 경우는
정사각형이나 직사각형의 타일에 대각선을 그은 뒤
색을 나누어 칠한다면 평행사변형(마름모) 모양의 타일을
만들 수 있습니다
아이와 색종이를 오려 다양한 타일 모양을 만들어 보세요
도형이나 공간에 대한 개념을 쉽게 이해시킬 수 있습니다.
출처- 캠브리지 체험수학 교육정보

https://blog.naver.com/ssisahoy
포스코 아이리더스쿨 : 네이버 블로그
-유치원2급, 1급, 원감, 원장자격증 취득, *<강서교육청 교육장>상 *< 서울특별시 교육감>상 수상 -교육게임 지도자 자격증 -독서지도사 -스토리텔링지도사 -초등수학 지도사-융합코딩지도사자격
blog.naver.com
'탐구수학 > 10세' 카테고리의 다른 글
| 사고력 수학/ 2025년 10세/ 쌓기나무/동탄 (0) | 2025.06.01 |
|---|---|
| 창의 사고력 수학/ 2025년 10세 지오보드/ 아이리더스쿨/동탄 (2) | 2025.03.30 |
| 창의 사고력 수학/ 2025년 10세 하트 퍼즐/ 아이리더스쿨/동탄 (0) | 2025.03.01 |
| 창의 사고력 수학/ 2025년 10세 칠교/ 아이리더스쿨/동탄 (0) | 2025.01.26 |
| 창의 사고력 수학/ 2024년 10세 성냥개비퍼즐/ 아이리더스쿨 (2) | 2024.12.02 |